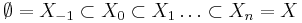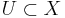Topologically stratified space

In topology, a branch of mathematics, a topologically stratified space is a space X that has been decomposed into pieces called strata; these strata are topological manifolds and are required to fit together in a certain way. Topologically stratified spaces provide a purely topological setting for the study of singularities analogous to the more differential-geometric theory of Whitney. They were introduced by René Thom, who showed that every Whitney stratified space was also a topologically stratified space, with the same strata. Another proof was given by John Mather in 1970, inspired by Thom's proof.

Definition

The definition is inductive on the dimension of X. An n-dimensional topological stratification of X is a filtration

of X by closed subspaces such that for each i and for each point x of

X_i \ X_i-1,

there exists a neighborhood

of x in X, a compact n-i-1-dimensional stratified space L, and a filtration-preserving homeomorphism

.

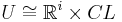Here 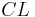is the open cone on L.

If X is a topologically stratified space, the i-dimensional stratum of X is the space

X_i \ X_i-1.

Connected components of X_i \ X_i-1 are also frequently called strata.

See also

• Singularity theory
• Whitney conditions
• Thom-Mather stratified space
• Stratifold
• Intersection homology

References

• Goresky, Mark; MacPherson, Robert Stratified Morse theory, Springer-Verlag, Berlin, 1988.
• Goresky, Mark; MacPherson, Robert Intersection homology II, Invent. Math. 72 (1983), no. 1, 77--129.
• Mather, J. Notes on topological stability, Harvard University, 1970.
• Thom, R. Ensembles et morphismes stratifiés, Bulletin of the American Mathematical Society 75 (1969), pp.240-284.
• Weinberger, Shmuel (1994). The topological classification of stratified spaces. Chicago Lectures in Mathematics. Chicago, IL: University of Chicago Press.